HF Radio Wave Propagation in the Earth’s Ionosphere

Gavin Ford | 2025-03-12

Background

As solar radiation from the sun reaches the upper atmosphere, the neural gases become ionized. This ionization forms a plasma which has important effects on radio wave propagation.

The ionosphere has several layers caused by varying electron densities. These electron densities vary throughout the day-night cycle and are at a maximum during the day.

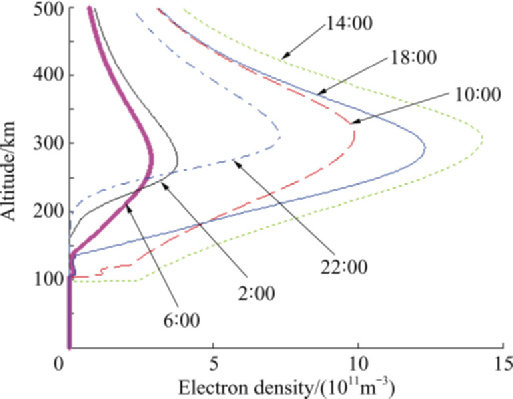
The plasma is the ionosphere causes the electromagnetic waves which are transmitted through it to change velocity. The phase velocity of the wave is given by the following equation.

$v=\frac{c}{\sqrt{1-(\frac{{\omega }_{pe}}{\omega })}}$

Where $v$ is the phase velocity, $c$ is the speed of light in a vacuum, $\omega$ is the frequency of the electromagnetic radiation, and ${\omega }_{pe}$ is the electron plasma frequency given by the following:

${\omega }_{pe}=\sqrt{\frac{n_e(y)e^2}{m_e{ϵ}_0}}$

Where $n_e(y)$ is the electron density as a function of altitude, $e$ is the elementary charge, $m_e$ is the mass of one electron, and ${ϵ}_0$ is the vacuum permittivity.

We can then solve for the velocity at any altitude:

$v(y)=\frac{c}{\sqrt{1-\frac{n_e(y)e^2}{m_e{ϵ}_0{\omega }^2}}}$

From equation (1), we can see that phase velocity of the electromagnetic wave will be greater than the speed of light. This is possible because the group velocity remains at the speed of light, which prevents breaking the universe.

Path Calculations

In an attempt to simplify the model, we will represent the electron density function, $n_e(y)$, as a linear function that increases to a maximum from 100 km to 300 km then decreases back to 0 until 500 km. Additionally, we will be ignoring the effects from the earth’s magnetic field.

Using Fermat’s principle, we can create the following functional then optimise to find the path the wave will follow.

$\int \frac{1}{v(y)\sqrt{1+{y^{\prime }}^2}}dx$

Using the Euler-Lagrange equation, we can find the minimal variation.

$C_1=F-y^{\prime }{F}_{y^{\prime }}$
$F_{y^{\prime }}=\frac{1}{v(y)}\frac{y^{\prime }}{\sqrt{1+{y^{\prime }}^2}}$

Solving for y' :

$C_1=\frac{1}{v(y)}(\sqrt{1+{y^{\prime }}^2}-\frac{{y^{\prime }}^2}{\sqrt{1+{y^{\prime }}^2}})$
$=\frac{1}{v(y)}(\frac{1+{y^{\prime }}^2}{\sqrt{1+{y^{\prime }}^2}}-\frac{{y^{\prime }}^2}{\sqrt{1+{y^{\prime }}^2}})$
$=\frac{1}{v(y)}(\frac{1}{\sqrt{1+{y^{\prime }}^2}})$
$(C_{1}v(y){)}^2=\frac{1}{1+{y^{\prime }}^2}$
$y^{\prime }=\sqrt{\frac{1}{(C_{1}v(y){)}^2}-1}$

We get a differential equation representing the slope of the propagation path at a given altitude.

Since the differential equation does not have a nice solution, I used python to numerically solve it. Following is the propagation path for each lift off angle from 0 to 89 degrees with a frequency of 7 MHz (40 meter band), and max electron density of $5\times {10}^{11}{m}^{-3}$:

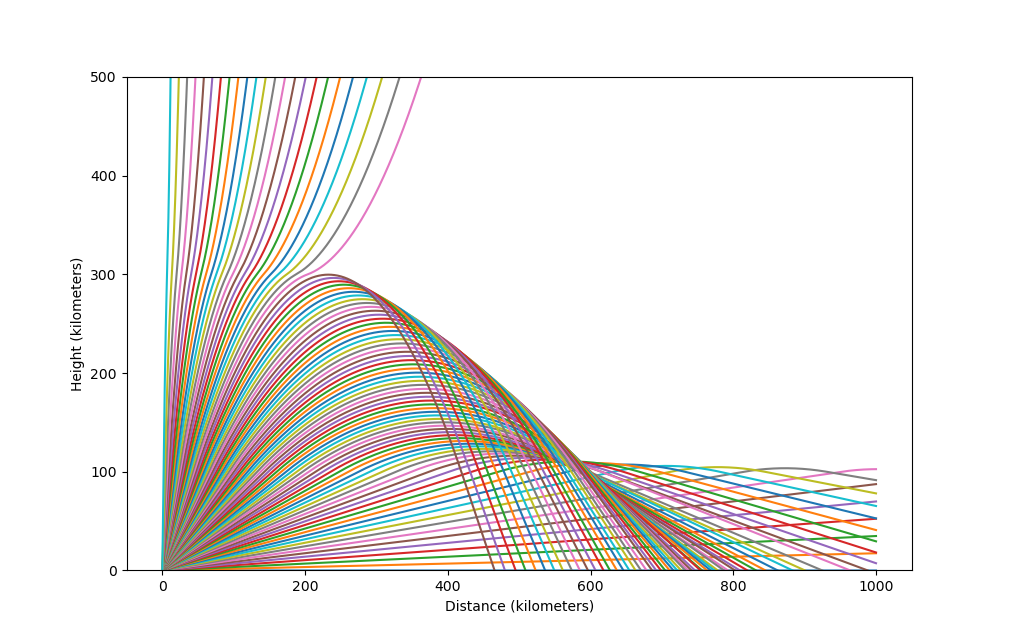
Conclusion

The properties of the ionosphere allow for HF radio waves to reflect off of it and reach farther distances than can be reached with direct ground wave propagation. At high angles, the waves make it through the ionosphere and do not get reflected. This causes a skip zone between where ground wave reaches and where the reflected wave reaches. These reflections allow HF radio to reach distances much farther than higher frequency radio waves.

References

Bilitza, D., Pezzopane, M., Truhlik, V., Altadill, D., Reinisch, B. W., & Pignalberi, A. (2022). The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Reviews of Geophysics, 60, e2022RG000792. https://doi.org/10.1029/2022RG 000792

Yan, Zhaowen & WANG, Gang & LI, Weimin & YU, Dapeng & Rahman, Toyobur. (2011). Prediction of Group Delay Distribution Around Receiving Point Using Modified IRI Model and IGRF Model. Chinese Journal of Aeronautics. 24. 797–806. 10.1016/ S1000-9361(11)60094-0. https://doi.org/10.1016/S1000-9361(11)60094-0.

29:129 -Plasma Oscillations-An application of electrostatics and classical mechanics. (n.d.). Retrieved March 11, 2025, from https://homepage.physics.uiowa.edu/~rmerlino/129Fall12/ 29_129_Plasma_oscillations.pdf